Summary
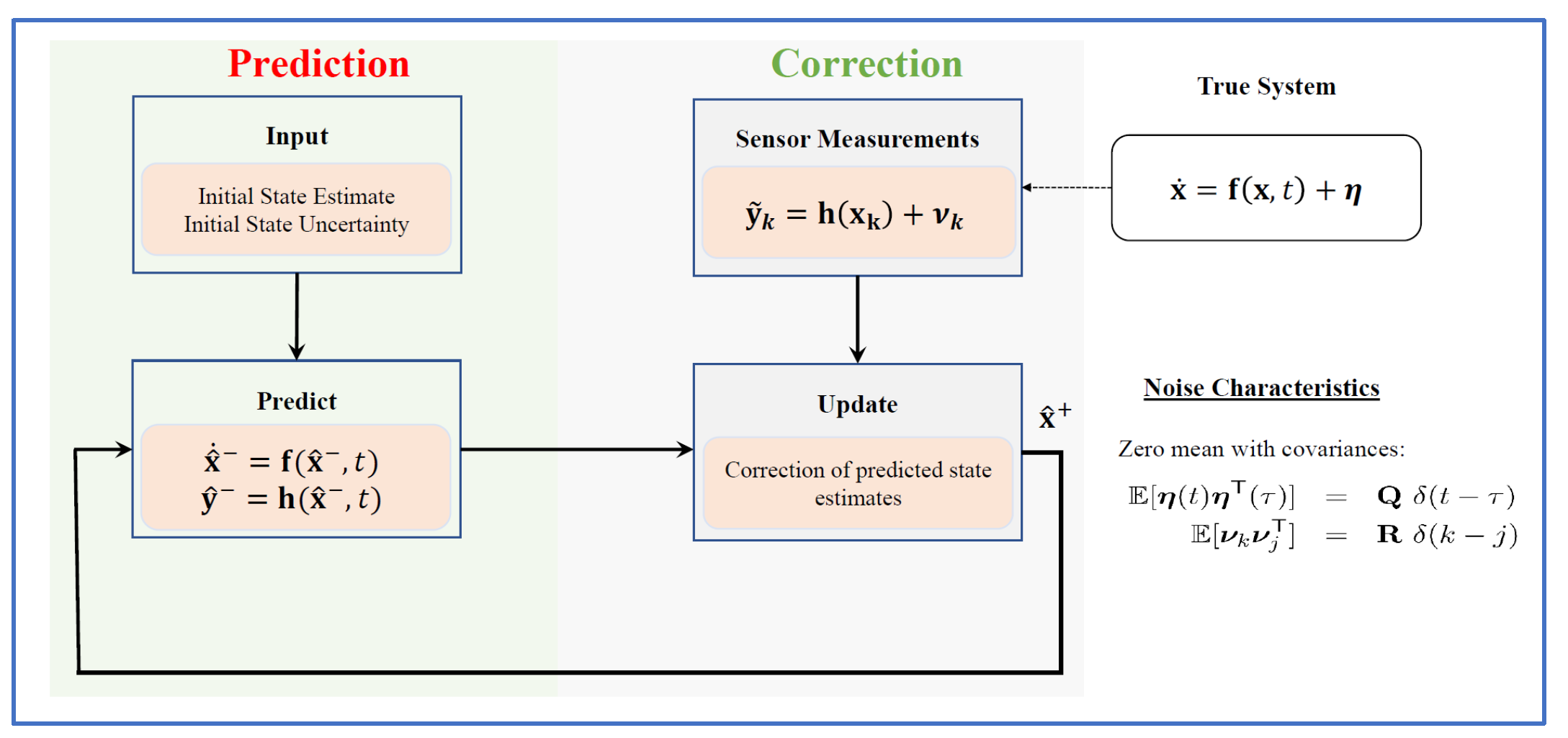
Precise estimation of the system states plays a vital role in many engineering applications, for example, robot navigation, spacecraft tracking, process monitoring, among others. State estimation involves both estimation and filtering using the governing system of equations and noisy observations of the system from available sensors. In real world situations, both the dynamical model and measurement model are significantly nonlinear. Often, the parameters of the system are also not known precisely, and the uncertain parameters have non-Gaussian distributions. The major challenge with the nonlinear filters in the literature lies in the efficient propagation of uncertainties in the filtering process, which can be addressed by developing a nonlinear filter in the generalized polynonial chaos(gPC) expansion framework. This motivates us to develop ensemble Kalman filter-based state estimator in the pseudospectral collocation-based gPC expansion framework. We propose a gPC expansion-based nonlinear filter for a system with continuous-time nonlinear dynamics and discrete-time nonlinear measurement model with uncertain initial states and parameters. The filter is developed in a prediction-correction form such that the predicted state estimates are computed using the gPC expansion-based uncertainty propagation. Also, upon arrival of the measurements, the predicted estimates are corrected in an ensemble Kalman filter setting. Using mixed-sparse grid ( MSG )-based pseudospectral collocation, the proposed filter can carry out state estimation for a nonlinear system with non-Gaussian uncertainties in the parameters and states.