Summary
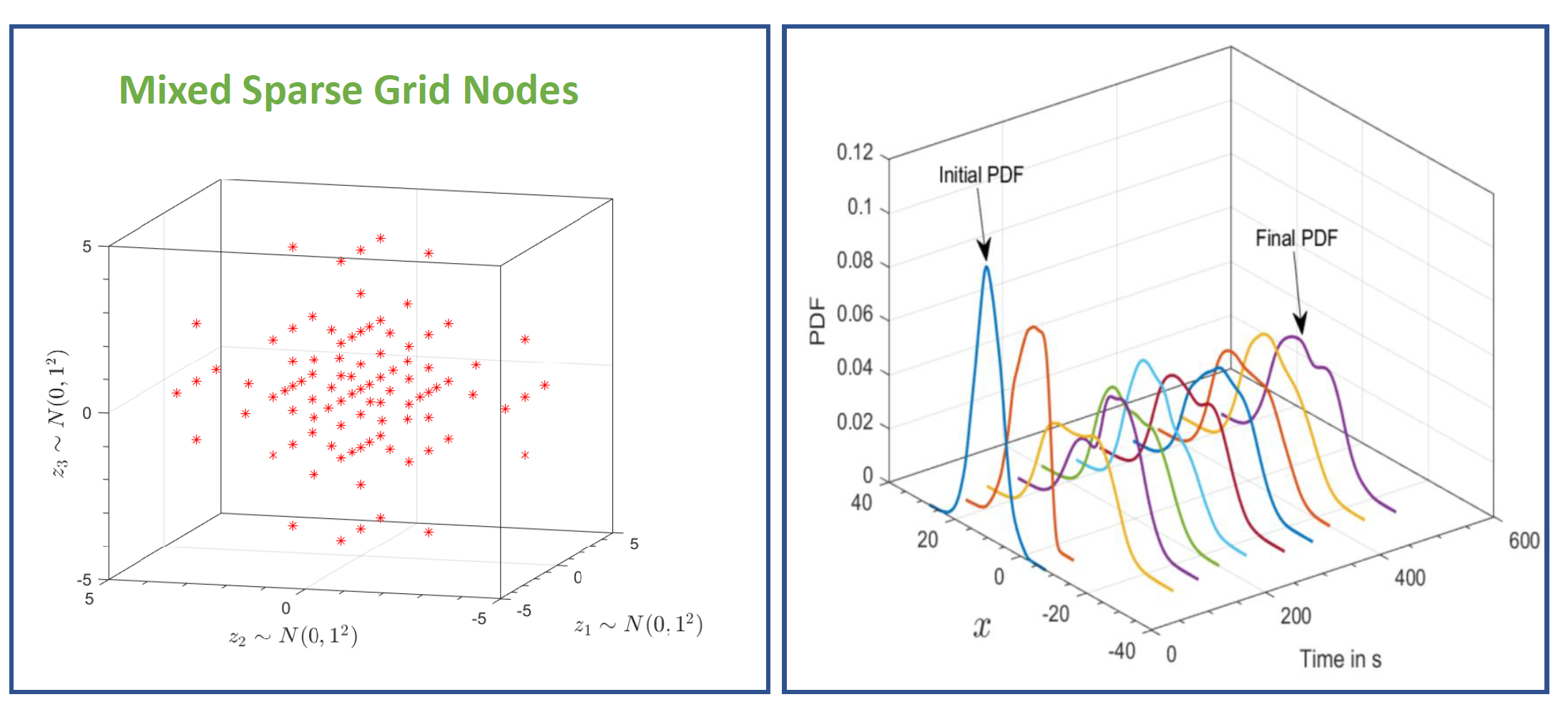
This research presents the use of generalized polynomial chaos (gPC) expansion for the propagation of uncertainties that are inherent in various dynamic system models in different forms. These stochastic dynamic models are pertinent in various engineering fields which include space situational awareness (tracking and data association related to resident space objects, conjunction assessment), relative navigation scenarios (target tracking, formation flying among aircraft, and autonomous rendezvous and docking of spacecraft), among others. In order to make informed decisions in preventing hazards and to mitigate the risks, it is of utmost importance to accurately characterize the uncertainties, study their evolution through probabilistic/statistical approaches, and analyze their impact on model response. The uncertainty propagation is carried out using pseudospectral collocation technique in gPC expansion framework. A novel quadrature-sampling technique, namely Mixed Sparse Grid (MSG) quadrature, is proposed to compute the collocation nodes for stochastic differential equations with underlying joint density function of Gaussian and uniform distributions. Nested one-dimensional quadrature rules are used for high-dimensional problems to further improve the efficacy of the proposed technique. This work also studies the long term degeneracy problem typically observed with gPC expansions of high order systems. The proposed numerical framework can mitigate this problem by selecting suitable accuracy level of MSG quadrature for a given order of gPC expansion.